我們常用的AC-DC開關電源中,由于初級線圈的漏感而再次級線圈上產生的瞬間反向脈沖是非常嚴重的。如下圖圖1,這是用MPS公司的MP020-5芯片搭建的AC-DC電路,這里測的是次級部分肖特基二極管兩端的波形。我們知道,肖特基二極管的的作用就是防止變壓器初級線圈的瞬態反向脈沖通過次級線圈對后級電路造成沖擊,如果在芯片啟動之后,后級肖特基二極管因為無法承受反向沖擊脈沖而造成短路,那么開關電源芯片會被瞬間擊穿。這里我是用的變壓器初級次級比值為1:3,而我們一般的反向瞬間脈沖約為700~1000V,甚至更多,我們根實際測得的波形可以看出,次級線圈的反向脈沖電壓為224V左右。我們在 很多的AC-DC電源方案中都可以看到肖特基二極管并聯一個RC電路,但是我們不知道這兩個元器件的值怎么去選,因為實際的設計中,我們不一定會按照方案中要求去選用一模一樣的變壓器,就比如MPS020-5推薦的變壓器匝數比為1:11,但是考慮到實際變壓器的體積,我們改為1:3,那么這個匝數比的改變會導致次級反向瞬間脈沖的不同,那么對于肖特基二極管的反向承受電壓就有一個嚴格的要求。那么如何能讓RC真正的起到作用而減少肖特基二極管的成本,或者說這個RC到底起一個什么作用。本文以實驗的角度和大家一起討論這個問題。
附:MP020-5開關電源原理圖
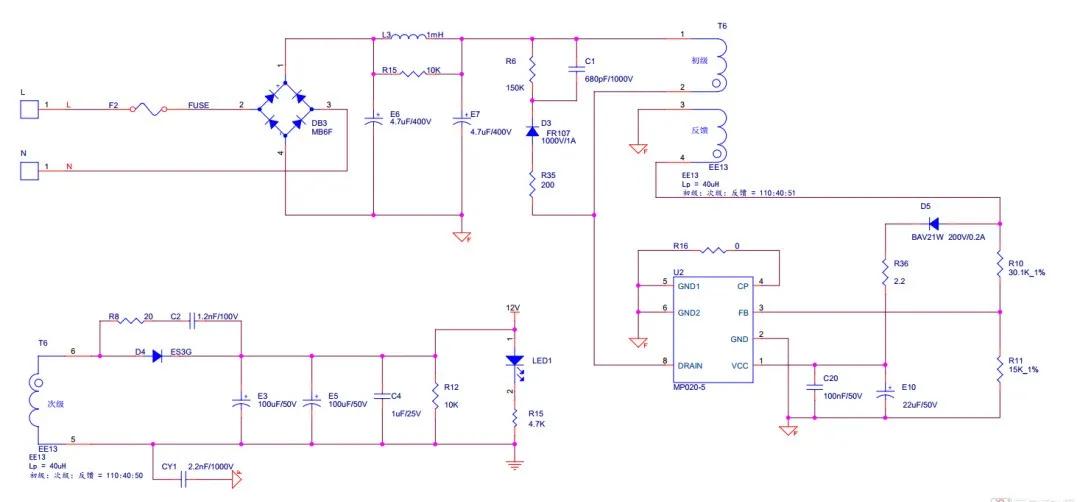

2、分析問題
從系統控制理論的角度出發,我們將這個次級的電路進行模型化,如圖2和圖3。
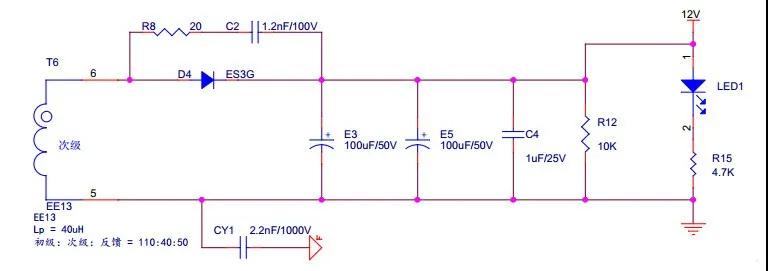
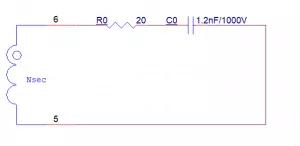


這里由于電容具有開關電源開啟瞬間短路的性質,所以R12和R15的后級都被短路了,等效電容C0為E3、E5電容并聯再與C2串聯。而電容串聯的計算是等效為 電阻并聯的計算,即串聯的電容越小,等效電容越小,所以我們直接按最小的電容C2進行計算,即等效電容C0為1.2nF,電感為變壓器的次級線圈,電阻R8(等效電阻為R0)為我們需要測定的值。
根據基爾霍夫電壓定律寫出RLC串聯諧振的微分方程,再進行拉普拉斯變化可以看出,這個模型我們可以發現這是一個RLC串聯諧振電路,在控制系統中這是一個典型的二階系統,具體的公式推導見圖4和圖5。
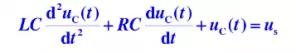
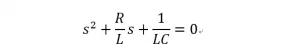
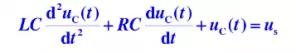
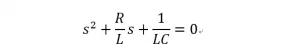
這是一個典型的二階連續系統,我們再次審視這個波形圖圖6可以發現,這是一個瞬態響應圖像。瞬態響應即在開關電源開啟的瞬間產生的響應。
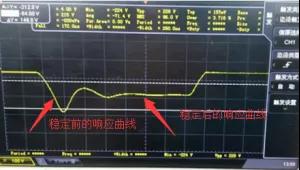

二階系統下,瞬態響應主要表現為三種狀態:欠阻尼、臨界阻尼、過阻尼。
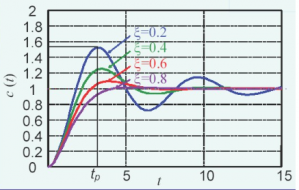

欠阻尼響應的曲線圖圖7
欠阻尼由于阻尼不夠,系統在響應瞬間會超過穩態值,然后慢慢的通過振蕩來跌落到穩態值,上圖的曲線表現出來的就是欠阻尼的狀態。也就是說,我們的電壓本來應該達不到224V,但是在一個慣性的作用下,系統在達到了穩定值之后超過了穩定值,達到了一個值,然后慢慢落下維持在穩定值的范圍內。
臨界阻尼響應的曲線圖圖8
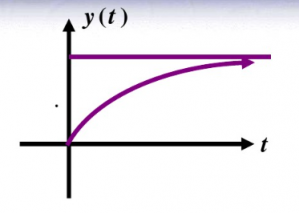

臨界阻尼下由于阻尼剛剛夠,系統在響應瞬間慢慢的上升到穩態值,不會產生慣性,我們的所需要的就是這樣一種波形。
RLC串聯諧振的拉普拉斯變換公式推導如圖圖9


我們通過電橋測得L的值為260mH,L的值為變壓器次級線圈的電感值,C為1.2nF,帶入求出電阻R為1658Ω。
3 測試驗證
根據得到的理論值可以得到在1658歐姆左右可以達到臨界阻尼,由于實際中手邊沒有1658歐姆的電阻,只有357歐姆,而焊盤只夠放兩個電阻串聯,所以我將兩個357歐姆的電阻串聯得到714歐姆的電阻,然后將電路進行測試。
可以看出系統在響應瞬間就很快的達到了穩態,而之前出現的欠阻尼的沖擊脈沖也被消除了,而反向電壓也被鉗制在-156V,當然了這個阻值不能太大,在達到一定的值之后,系統會越過臨界阻尼,這個電阻的選值是一個范圍。另外還有一個就是這里的電容也要盡量的小,在nF級,如果太大會造成芯片爆炸。總的來說,在確定好RC的值之后,我們可以有效的抑制次級反向脈沖由于慣性對肖特基二極管造成的更大的電壓沖擊。這樣做的好處可以讓我們理解RC存在的理由,當然還可以節約物料成本。之前使用的物料為SS320肖特基二極管,反向承受電壓為200V,經常爆板,后來使用了ES3G,反向承受電壓為400V,雖然可以用但是物料比較貴。通過這種簡單的辦法可以更好的節約成本。
烜芯微專業制造二極管,三極管,MOS管,橋堆等20年,工廠直銷省20%,4000家電路電器生產企業選用,專業的工程師幫您穩定好每一批產品,如果您有遇到什么需要幫助解決的,可以點擊右邊的工程師,或者點擊銷售經理給您精準的報價以及產品介紹
烜芯微專業制造二極管,三極管,MOS管,橋堆等20年,工廠直銷省20%,4000家電路電器生產企業選用,專業的工程師幫您穩定好每一批產品,如果您有遇到什么需要幫助解決的,可以點擊右邊的工程師,或者點擊銷售經理給您精準的報價以及產品介紹


